EECS70 Notes

CS70: Discrete Math

Set Theory

Sets consist only of unique elements
$\mathbb{Z}$: Set of all Integers = $\{..., −3, −2, −1, 0, 1, 2, 3, \ldots\}$
$\mathbb{N}$: Set of all natural numbers = $\{ |a| : a \in \mathbb{Z}\}=\{ 0, 1, 2, 3,\ldots\}$, it and subsets are countably infinite
$\mathbb{R}$: Set of all real numbers = everything not complex
$\mathbb{Q}$: Set of all rational numbers = $\{p/q : p \in \mathbb{Z}, q \in \mathbb{N}\}$. Set of all irrational numbers $= \mathbb{R} \backslash \mathbb{Q}$
Cardinality of a set S = |S| = Number of elements in set S
Subsets: Everything in subset is in superset, $A \neq B\implies B$ is a proper subset.
Union:
$A \cup B, \{x: x \in A \lor x \in B\}$
All the elements in set $A \lor$ in set $B$
Intersection:
$A\cap B, \{x: x \in A \land x \in B\}$
All the elements in set A and in set B
Set Difference:
$A \backslash B = A-B = \{x: x \in A, x \not\in B\}$
All the elements in set A not in set B
Cartesian Product:
$A \times B = \{(x,y): x\in A, y\in B\}$
If $A \cap B = \varnothing = \{\} = $ Empty Set, then A and B are disjoint sets
Example: even and odd numbers
Complements:
$A^c = A' = Ā:$ everything in the universe that’s not in a set
$A^c = \{x: x\not\in A, x\in \mathbb{U}\}$
Universes:
$\mathbb{U} =$ The set of all elements that we are looking at
DeMorgan’s Laws:
$(A \cap B)^c \equiv A^c \cup B^c$
$(A \cup B)^c \equiv A^c \cap B^c$
XOR: Exclusive Or
$A \oplus B = (A \lor B) \land (\lnot A \lor \lnot B$)

Logic & Proofs

Conjunction: and $=\land$. Disjunction: or $=\lor$
Proposition is either true or false (has no free variables): $(P \implies Q) =($ If p, then Q $)=(\lnot P \lor Q)$
Direct Proofs: Mainly used for proving implications $(P\implies Q)$. Assume $P$ then prove $Q$.
Contrapositive $=\lnot Q\implies\lnot P$. Equivalent to proposition. Assume $\lnot Q$ then prove $\lnot P$.
Contradiction: Assume $\lnot(P\implies Q)\equiv (P\land\lnot Q)$ and get a contradiction.
Proof by cases: Split claim into cases which cover entirety of the domain.
Converse $= (Q \implies P) \iff (\lnot P\implies\lnot Q) =$ Inverse. Not equiv to implication.
Absorption Rule: $P \lor (P \land Q) \equiv P \land (P \lor Q) \equiv P$
Tautology: always true. Contradiction: always false

If and only if: $(A\text{ iff }B) = (A\iff B) = ((P \implies Q) \land (Q \implies P))$
Quantifiers: for all $\forall,$ there exists $\exists$ ($\exists$ is fluid for $\lor$ but not $\land$)
Induction:
Base Case:
(usually $n=0\lor n=1$)
Show LHS=RHS $\therefore$ base case holds
Induction hypothesis:
Assume holds for $n=k$ where $k\in(\sup n)$
Induction step:
Prove $P(k)\implies P(k+1)\therefore$ induction holds (use IH to do so)
Strong Induction: Assume previous values are true for $(\sup n) \leq n \leq k$ then prove $P(k)\implies P(k+1)$.

Stable Matching:

Propose-and-Reject Algorithm:
Every Morning: Each job proposes (i.e. makes an offer) to the most preferred candidate on its list who has not yet rejected this job.
Every Afternoon: Each candidate collects all the offers she received in the morning; to the job offer she likes best among these, she responds “maybe” (she now has it in hand or on a string), and to the other offers she says “no” (i.e., she rejects them). (This is just a way for us to virtually model that there are no “exploding offers” and a job can’t withdraw an offer once an offer is made.)
Every Evening: Each rejected job crosses off the candidate who rejected its offer from its list. The above loop is repeated each successive day until there are no offers rejected. At that point, each candidate has a job offer in hand (i.e. on a string); and on this day, each candidate accepts their offered job (i.e. the job offer she has in hand) and the algorithm terminates.
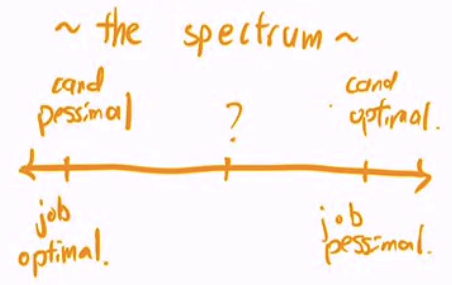
Job propose and reject produces a job-optimal pairing (and candidate pessimal pairing)
Optimal: best stable outcome
Pessimal: worst stable outcome

if there is only one stable matching then it is all of the 4 above
Improvement Lemma:
well-ordering principle:
every non empty subset of the positive integers has a least element -

Graph Theory:

Graph: $G = <V, E>$
Connected Graph: if there is a path between any two distinct vertices
If G is connected and has no edges $\implies |E_G| = |V|-1$.
Connected Components: sets of connected vertices
Incident: vertices an edge touches
Adjacent/Neighbors: vertices that are connected by edges
Isolated: vertex of degree 0
Degree of a vertex: number of edges attached to a vertex
Simple graph: undirected graph with no loops/multiple edges to a vertex
Closed: start=end. Else open.

Name	Definition	No repeat edges	No repeat vertices	Same 1st + last node	Visits every edge once	Visits every vertex once
Simple Path	Sequence of connected edges with distinct vertices	X	X
Cycle (or circuit)	Simple path with v1 = vk; all cycles are tours	X	X	X
Walk	any sequence of connected edges: $\{v_1, v_2\}, \{v_2, v_3\}, \{v_3, v_4\}\ldots$
Tour	walk that starts and ends at same node	X		X
Eulerian Walk	connected and at most two odd degree vertices	X			X
Eulerian Tour	iff connected and every vertex has even degree (allows isolated vertices)	X		X	X
Hamiltonian Walk	contains \|V\|-1 edges	X	X			X
Hamiltonian Tour	all hypercubes have one, contains \|V\| edges	X	X	X		X

Tree: an acyclic graph where any edge addition creates a cycle
a connected graph without a cycle
a connected graph with |V| − 1 edges
a connected graph where any edge removal disconnects it
Planar: Can be drawn with no edge crossings, $\implies (e\leq 3v-6)\lor (v+f=e+2)$.
Prove planar: Does not contain $K_{3, 3} \lor K_5$.
Bipartite: two-colorable, no odd length cycles, can be split into left and right
Hypercubes: n-dimensional hypercube is made of 2 (n-1)-d hypercubes. Proofs use reverse on 1 (n-1)-d subcube.

Modular Arithmetic:

Division Algorithm:

$a\mid b \iff (∃q \in \mathbb{Z}, b = aq)$
$n = dq + r$ where $0 \leq r < q,q\in\mathbb{Z}. \implies (a \equiv b \pmod m \iff m \mid (a - b))$
n: dividend
d: divisor
q: quotient
r: remainder
Seen in algebra as: $\frac n d = q + \frac r d$
Any even integer can be expressed as $2k, k\in\mathbb{Z}$
Any odd integer can be expressed as $2k + 1, k \in \mathbb{Z}$
Fundamental Theorem of Arithmetic: prime factorization exists
GCD: min of prime factorization powers, LCM: max of prime factorization powers. $\text{lcm}(a,b)=\frac{|a\cdot b|}{\gcd(a,b)}$

Euclid’s: $d=\gcd(x, y) = \gcd(y, x \pmod y) = \exists a,b: ax+by$
Modular inverses $(\exists a^{-1} \iff \gcd(a, m) = 1)\implies(\exists x: ax \equiv 1 \pmod m)$
Fermat’s Little Theorem:
For prime $p, a^{p-1} \equiv 1 \pmod p$
CRT: If moduli are coprime

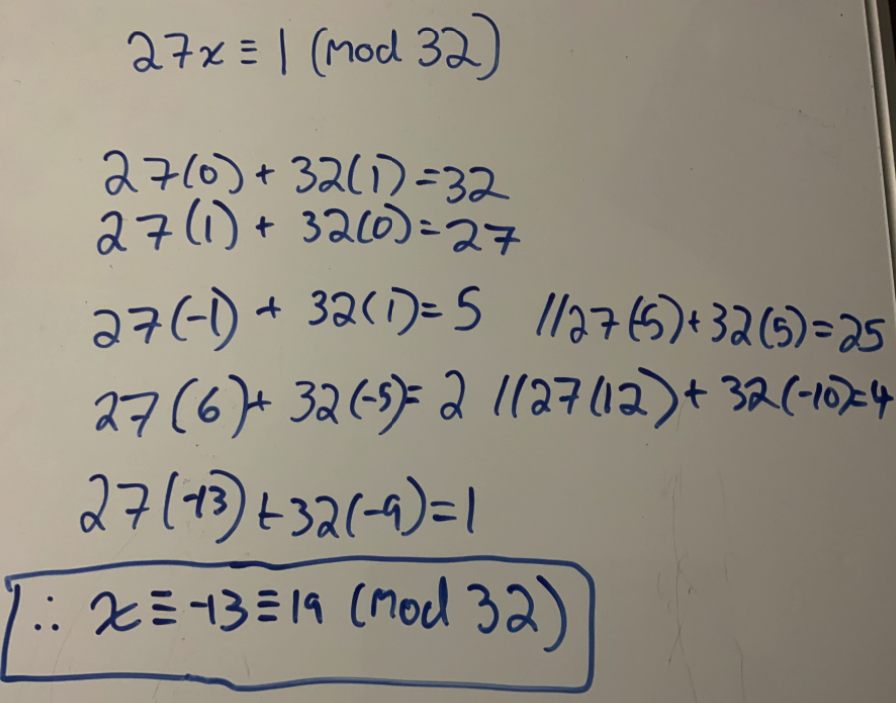
RSA:

$N=p\cdot q$
$e$ is relatively prime to $(p-1)(q-1)$ (so an inverse exists). Usually $e=3 \lor e=2^{16}+1=65537$.
Public key: $(N, e)$
Private key: $d$, $d \equiv e^{-1} \pmod{(p−1)(q−1)}$.
$E(x) = x^e \pmod N$ and sends this to Bob.
Given $y = E(x)$, computing $D(y) = y^d \pmod N$ will give back x as $D(E(x))=x \pmod N$.
Efficiency: comes from repeated squaring

Bijections

Injection
all y are are used ≤ 1
each element in the codomain is pointed to at most once
|A| ≤ |B|
one-to-one
Proofs:
horizontal line test
derivative test (if always incr/always decr)
MUST HAVE SIGN CHANGE
f(a)=f(b) \implies a=b
To disprove injectivity:
Pigeonhole Principle:
Let n and k be positive integers. Place n objects into k boxes. If n > k, then at least one box must contain multiple objects
Surjective
all y are used ≥ 1 (codomain=range)
each element in the codomain is pointed to at least once
|A| ≥ |B|
onto
Does range cover codomain exactly?
Polynomials of odd degree are always surjective with codomain $\mathbb{R}$
Bijection
all y are used exactly once
|A| = |B|
one-to-one and onto
surjection + injection
iff ∃ multiplicative inverse

Polynomials

Uniqueness Fact: Given $d+1$ points, you can construct at most 1 degree d polynomial
Example: given 2 points, once can construct a line (which has degree 1)
Roots Fact: Any nontrivial degree d polynomial has at most d roots
where the trivial polynomial is defined as $y=0$
Examples: A line (degree 1) has at most 1 root, a quadratic (degree 2) has at most 2 roots
If $f$ and $g$ are non-zero real polynomials then the roots are:
$0 \leq f + g \leq \max(\text{deg}_f, \text{deg}_g)$
$0 \leq f \cdot g \leq (\text{deg}_f + \text{deg}_g)$
$0 \leq f / g \leq (\text{deg}_f - \text{deg}_g)$

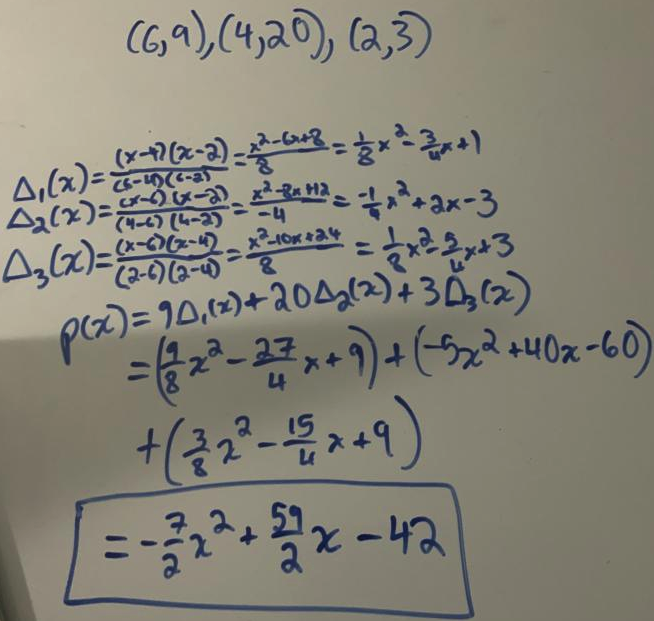
Fields:

Modulo arithmetic with a prime moduli is a "field"

Counting

the number of sequences of $k$ cards $=52\times 51\times ··· \times [52−(k −1)]$
First Rule of Counting: total number of distinct objects $= n_1 \times n_2 \times n_3 \times ··· \times n_k$ where $n_i$ is the branching factor
Binomial Coefficient $ = \frac{n!}{(n-k)!k!} = {n\choose k}$ = the number of ways of choosing k objects out of a total of n distinct objects, where the order of the choices does not matter.
Second Rule of Counting: Assume an object is made by a succession of choices, and the order in which the choices are made does not matter. Let A be the set of ordered objects and let B be the set of unordered objects. If there exists an m-to-1 function f from A to B, we can count the number of ordered objects (pretending that the order matters) and divide by m (the number of ordered objects per unordered objects) to obtain |B|, the number of unordered objects
Stars and bars: $\binom{n+k-1}{n}$

Probability Theory:

P(A U B) = P(A) + P(B)
P(A^B)
Baye’s theorem: Probability of A given B:
P(A|B) = P(A n B) / P(B) = P(B|A)*P(A)/P(B)